台球二向法瞄点击球

前言

缘起

这个方法是几年前我脑洞乱开，用最基本的初中几何知识，基于传统的台球碰撞原理，在纸上瞎比划了一下，然后转化成了极简的几小步而成型。

原理

其实这个方法的原理没有任何稀奇，都是各种经典教程已经说烂的“碰撞一瞬间，两球心和洞口，三点一线”，这种基本的规律不太可能创新。

传统方法的缺点

很多经典的方法，比如分厚薄记参数，假想球找尾巴，杆头定点等等，要么特别麻烦，要么非常凭感觉。总之就是不好用，而且不确定性太大。

二向法的优势

1. 甩掉口诀参数，无视角度大小；
2. 步骤简单直观，一看就会，甚至不用动脑子；
3. 对立体空间思维没有要求。

总之就是简单，而且不用凭感觉。

为啥叫“二向法”

因为这个方法最大的贡献，就是将瞄球这件事，从三维空间转化为二维平面（致敬大刘《三体》里的神器：二向箔），由需要凭感觉的“玄学”变为确定的“科学”。所有操作不需要立体空间思维，只用在平面上进行思考。

二向法介绍

观察局势确定进球目标

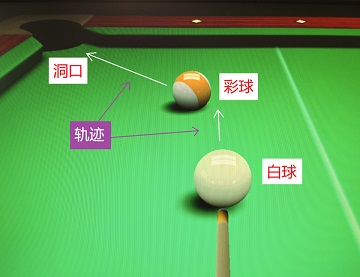
确认【白球】、【彩球】和【洞口】，估计大概的运动轨迹：

找到进球点

1. 站在和彩球、洞口三点一线的位置；
2. 低下头观察，当彩球刚好把洞口挡住时，彩球的【圆心】就是进球点；
3. 记住这个点在【彩球表面上的位置】，通常可以根据周边的花纹来辅助记忆（比如这张图的进球点刚好在彩条区域的中线附近），没有花纹就强行记忆（其实球表面反射的灯光倒影也可以用来辅助）。

找到对称假想圆

错误方法

很多人到这一步，就将白球直接正对着进球点打过去，这其实是不准确的（实际上对小于 30 度的小角度球可以应付，大角度就很不准了）。

正确方法

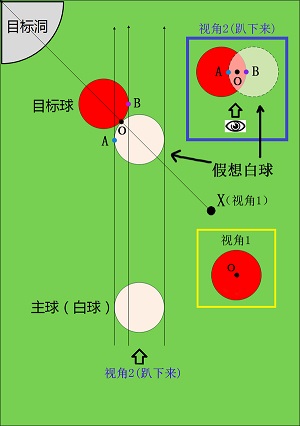
1. 回到白球的的位置，低头观察，找到刚才的进球点位置（标记为S点）；

   

2. 将彩球标记为A圆，找到A圆最右边的点（标记为M点）；

   

3. 将S点作为中心点，找到M的对称点N（S点离M、N两点的距离相等）;

   

4. 想象一个和A圆大小完全相同的B圆，N点是B圆最左边的点 （此时，A圆和B圆相交区域的中心点就是S点，即A和B关于S对称），那么假想的B圆位置就是白球实际上应该去的位置。

   

5. 白球正对B圆打过去，就是把B圆当做一个目标球，然后打直球就可以了。

二向法总结

以上步骤，简单来说就是：

• 找到进球点

• 想象对称圆

• 正碰假想圆

就是这么简单，本人认为瞄准的好方法有两种：

1. 操作最简单上手最快的 — 二向法

   非常简单好用，但这个方法限于技法层面，属于“剑宗”；

2. 最麻烦也是上手最慢的 — 硬着头皮，只凭感觉打

   经历各种角度各种位置关系的长期大量实践，不断记忆感觉和修正感觉，到后来达到像职业选手一样看一眼就知道朝哪里打的程度，完成内化，这是最高境界，此为“气宗”。

原理图

下面是自己当时比划的原理图，有兴趣的可以琢磨一下，原理就是初中几何里最简单的两圆相切。